Fourier Transfrom, window

*푸리에 급수는 주기신호의 주파수 성분을 분석하는데 사용, 푸리에 변환은 비주기신호의 주파수 성분 분석에 사용

---

1. 푸리에 변환(Fourier transform, FT)

• 시간이나 공간에 대한 함수를 시간 또는 공간 주파수 성분으로 분해하는 변환을 말한다.
• 푸리에 변환은 이 변환으로 나타난 주파수 영역에서 함수를 표현한 결과물을 가리키는 용어로도 종종 사용된다. 
• 푸리에 변환된 결과물로부터 피변환함수를 복원할 수도 있고, 이를 증명하는 정리를 푸리에 역변환 정리라고 한다.
• 엄밀히 말하면 푸리에 변환은 일종의 적분 변환

---

 

 

[푸리에 변환을 사용하는 이유]

: 원래 함수에 적용할 수 있는 선형 연산은 주파수 영역에도 그 대응되는 연산이 존재하는데, 때때로 이 대응되는 선형 연산이 더 간단할 수도 있다. (즉, 더 단순한 함수와 연산은 현대 수학에 폭 넓게 응용되고 있음)

• 시간 영역에서 미분은 주파수 영역에서는 주파수와의 곱셈으로 나타나기 때문에 미분방정식을 푸리에 공간으로 옮겨와 푸는 경우도 종종 발생한다. 
• 또 시간 영역에서의 합성곱은 주파수 영역으로 옮겨오면 평범한 곱셈과 같다. 이런 경우에는 원 함수를 푸리에 공간으로 옮겨와 여기서 선형연산을 적용한 뒤, 다시 역변환을 통해 원 함수를 복원하는 방식으로 연산을 더 쉽게 적용할 수 있다. 

(영상으로 이해하기)

https://commons.wikimedia.org/wiki/File:Fourier_transform_time_and_frequency_domains_(small).gif

File:Fourier transform time and frequency domains (small).gif - Wikimedia Commons

---

 

 

[푸리에 변환의 단점?]

• 푸리에 변환은 시간에 대한 함수 또는 신호를 주파수 성분으로 분해하는 작업이다.
• 그러나 이렇게 변환하게 되면 '전체 시간'에 대해 주파수가 분석되기 때문에 각 주파수가 시간적으로 언제 존재하는 것인지 알 수 없다는 한계가 있다.
• 예를 들어, 음성처럼 시간마다 주파수가 변하는 데이터가 있다면? 0~10초까지는 5Hz, 10~20초까지는 10Hz인 것과, 0~20초까지 5Hz와 10Hz가 공존하는 신호를 구별해낼 수 있을까?
• 안타깝게도 푸리에 변환은 이런 신호를 구별해낼 수 없다. 이런 문제를 해결하기 위해 STFT(Short Term Fourier Transform)을 거쳐 WT(Wavelet Transform)이 등장한다

 => wavelet 변환이 등장

 

 

---

푸리에 변환의 정의와 한계에 대해 알아봤고,

대안책으로 나온 STFT, WT는 아래 블로그 보기 

 

 

https://m.blog.naver.com/dusrnwk/221799478508

웨이블릿 변환(Wavelet Transform)

https://www.youtube.com/watch?v=QX1-xGVFqmw

 

 

(이 강의도 좋음)

https://www.youtube.com/watch?v=jnxqHcObNK4

 

 

 

---

2. Window 

 

[FFT, frequency leakage] 

https://famtech.tistory.com/236

 

https://famtech.tistory.com/236

https://famtech.tistory.com/236

---

 

그림 1 : Hamming 함수(파랑)과 Hanning 함수(빨강)의 예

 

 

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=lecroykorea&logNo=221549211257

 

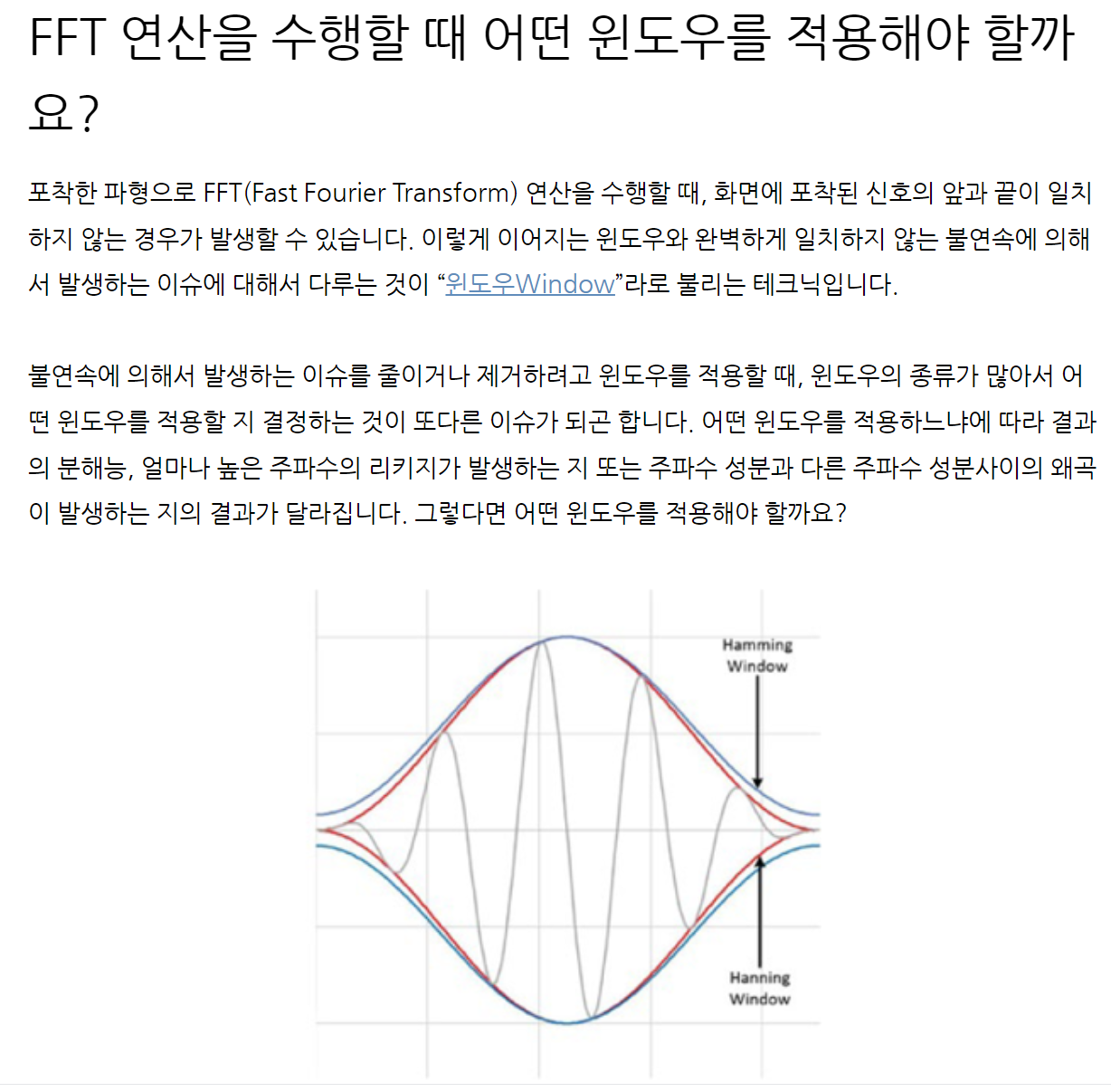
위 그림은 몇 가지 자주 사용되는 윈도우 함수들의 주파수 응답 곡선이다.

맨위는 윈도우를 적용하지 않은 것이고, 바로 아래의 초록색은 Hamming 윈도우 함수를 적용한 플롯이다. 그리고 다음에 보이는 것이 Hanning 윈도우를 적용한 결과이다. 특별한 이유가 없다면, 양호한 분해능과 높은 주파수 리키지가 낮아 적절한 균형을 이루고 있는 Hanning 윈도우가 적절하다.

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=lecroykorea&logNo=221549211257